kd-treeを実装してみた
はじめに
kd-treeを実装してみました
最近仕事でよく使うので勉強がてら
ソースコード
以下に公開してあります
github.com
kd-treeの構築と、以下の探索機能を実装してます
- 最近傍探索 (Nearest neighbor search)
- k-最近傍探索 (K-nearest neighbor search)
- 半径内に含まれる近傍の探索 (Radius search)
あと、ヘッダ1個includeするだけで使えるのでお手軽です
アルゴリズム
kd-treeの構築
wikipediaに載ってる疑似コードが分かりやすかったので引用させていただきます
function kdtree (list of points pointList, int depth) { if pointList is empty return nil; else { // 深さに応じて軸を選択し、軸が順次選択されるようにする var int axis := depth mod k; // 点のリストをソートし、中央値の点を選択する select median from pointList; // ノードを作成し、部分木を構築する var tree_node node; node.location := median; node.leftChild := kdtree(points in pointList before median, depth+1); node.rightChild := kdtree(points in pointList after median, depth+1); return node; } }
一方私の書いたコードはこんな↓感じです
Node* buildRecursive(int* indices, int npoints, int depth) { if (npoints <= 0) return nullptr; const int axis = depth % PointT::DIM; const int mid = (npoints - 1) / 2; std::nth_element(indices, indices + mid, indices + npoints, [&](int lhs, int rhs) { return points_[lhs][axis] < points_[rhs][axis]; }); Node* node = new Node(); node->idx = indices[mid]; node->axis = axis; node->next[0] = buildRecursive(indices, mid, depth + 1); node->next[1] = buildRecursive(indices + mid + 1, npoints - mid - 1, depth + 1); return node; }
疑似コードとほとんど同じです
私の場合は点そのものではなく、点へのインデックスをノードに保持しています
(中央値を取得するためにnth_elementを初めて使った…)
最近傍探索
k-d treeが構築できたらlet's最近傍探索
ググってヒットしたこちらの資料をもとに実装しました
(URLを見るとスタンフォード大の宿題らしい)
https://web.stanford.edu/class/cs106l/handouts/assignment-3-kdtree.pdf
原理は2分探索と同じで、「探している値は木の半分のこっち側にあるよね」
ってのを繰り返しながら左か右の子ノードに降りていきます
その過程で現在ノードとクエリとの距離を計算し最近傍の値を更新します
葉までたどり着いたら、自分の兄弟ノード(親から見て自分が左だったら、右のノード)の方に
最近傍の可能性がないかチェックして、ある場合は兄弟ノードの方も探索します
void nnSearchRecursive(const PointT& query, const Node* node, int *guess, double *minDist) const { if (node == nullptr) return; const PointT& train = points_[node->idx]; const double dist = distance(query, train); if (dist < *minDist) { *minDist = dist; *guess = node->idx; } const int axis = node->axis; const int dir = query[axis] < train[axis] ? 0 : 1; nnSearchRecursive(query, node->next[dir], guess, minDist); const double diff = fabs(query[axis] - train[axis]); if (diff < *minDist) nnSearchRecursive(query, node->next[!dir], guess, minDist); }
K-近傍探索や半径探索も探索の流れは同じです
デモ
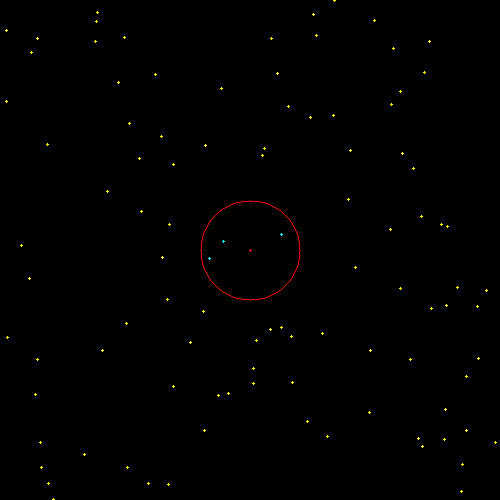
最近傍探索/k-最近傍探索/半径探索を実行した結果です
赤い点がクエリ(画像の中心座標)、青い点が近傍点になります


ARM NEONの使い方 除算編
四則演算ラスト!
今回は除算編です
アーキテクチャによる違い
32bit ARM
32bit ARMには除算を直接行うSIMD命令がないため
a/bという除算を行う場合、まず逆数を計算するSIMD命令によってbの逆数を計算し
これをaと掛け算することによって除算を表現します
64bit ARM
64bit ARMには除算を行うSIMD命令が追加されています
逆数の計算
vrecpe[q]_f32(va)
32bit浮動小数ベクタvaの各要素の逆数の近似値を計算します
近似値なのでCPU(IEEE754)よりも精度が低いです
サンプル
32bit浮動小数ベクタva, vbの除算をva*(vbの逆数)という形でやってみます
vaとvbの各レーンを同じ値に設定しているので、除算後の値が1になるのが望ましい結果です
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> static void print_vector(float32x4_t value) { float lane[4]; vst1q_f32(lane, value); for (int i = 0; i < 4; i++) printf("lane[%d]: %f\n", i, lane[i]); } int main() { float a[4] = { 1, 2, 3, 4 }; float b[4] = { 1, 2, 3, 4 }; float32x4_t va = vld1q_f32(a); float32x4_t vb = vld1q_f32(b); float32x4_t vrecipb = vrecpeq_f32(vb); // approximate reciprocal of vb float32x4_t vc = vmulq_f32(va, vrecipb); printf("va:\n"); print_vector(va); printf("\nvb:\n"); print_vector(vb); printf("\n1/vb:\n"); print_vector(vrecipb); printf("\nva * (1/vb):\n"); print_vector(vc); return 0; }
実行結果
va: lane[0]: 1.000000 lane[1]: 2.000000 lane[2]: 3.000000 lane[3]: 4.000000 vb: lane[0]: 1.000000 lane[1]: 2.000000 lane[2]: 3.000000 lane[3]: 4.000000 1/vb: lane[0]: 0.998047 lane[1]: 0.499023 lane[2]: 0.333008 lane[3]: 0.249512 va * (1/vb): lane[0]: 0.998047 lane[1]: 0.998047 lane[2]: 0.999023 lane[3]: 0.998047
近似値なので結構精度低いなーという印象
まあ用途次第でしょうけど
ベクタ逆数のステップ
よくわからないタイトルですが
先ほどの逆数の精度を良くする方法です
vrecps[q]_f32(va)
ARM Information Centerの説明が以下です
VRECPS (ベクタ逆数のステップ)は、あるベクタの要素を対応する別のベクタの要素で乗算し、その結果を 2 から減算して、最終的な結果をデスティネーションベクタの要素に返します。
最初この説明を見たときはなんのこっちゃと思いましたが
ニュートン法で逆数の近似を求める際に使うようです
ある数とその逆数の現在の近似値
があるとき、ニュートン法によって
という反復を繰り返すことで近似値がに収束します
このを計算してくれるのがvrecpsというわけ
サンプル
先ほどの逆数のサンプルにニュートン法の反復計算を追加してみました
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> static void print_vector(float32x4_t value) { float lane[4]; vst1q_f32(lane, value); for (int i = 0; i < 4; i++) printf("lane[%d]: %f\n", i, lane[i]); } int main() { float a[4] = { 1, 2, 3, 4 }; float b[4] = { 1, 2, 3, 4 }; float32x4_t va = vld1q_f32(a); float32x4_t vb = vld1q_f32(b); float32x4_t vrecipb = vrecpeq_f32(vb); // approximate reciprocal of vb float32x4_t vc = vmulq_f32(va, vrecipb); printf("va:\n"); print_vector(va); printf("\nvb:\n"); print_vector(vb); printf("\n1/vb:\n"); print_vector(vrecipb); printf("\nva * (1/vb):\n"); print_vector(vc); // Newton-Raphson iteration int steps = 3; for (int i = 0; i < steps; i++) { printf("\nNewton step: %d\n", i + 1); float32x4_t vtmp = vrecpsq_f32(vb, vrecipb); vrecipb = vmulq_f32(vrecipb, vtmp); vc = vmulq_f32(va, vrecipb); printf("\n1/vb:\n"); print_vector(vrecipb); printf("\nva * (1/vb):\n"); print_vector(vc); } return 0; }
実行結果
va: lane[0]: 1.000000 lane[1]: 2.000000 lane[2]: 3.000000 lane[3]: 4.000000 vb: lane[0]: 1.000000 lane[1]: 2.000000 lane[2]: 3.000000 lane[3]: 4.000000 1/vb: lane[0]: 0.998047 lane[1]: 0.499023 lane[2]: 0.333008 lane[3]: 0.249512 va * (1/vb): lane[0]: 0.998047 lane[1]: 0.998047 lane[2]: 0.999023 lane[3]: 0.998047 Newton step: 1 1/vb: lane[0]: 0.999996 lane[1]: 0.499998 lane[2]: 0.333333 lane[3]: 0.249999 va * (1/vb): lane[0]: 0.999996 lane[1]: 0.999996 lane[2]: 0.999999 lane[3]: 0.999996 Newton step: 2 1/vb: lane[0]: 1.000000 lane[1]: 0.500000 lane[2]: 0.333333 lane[3]: 0.250000 va * (1/vb): lane[0]: 1.000000 lane[1]: 1.000000 lane[2]: 1.000000 lane[3]: 1.000000 Newton step: 3 1/vb: lane[0]: 1.000000 lane[1]: 0.500000 lane[2]: 0.333333 lane[3]: 0.250000 va * (1/vb): lane[0]: 1.000000 lane[1]: 1.000000 lane[2]: 1.000000 lane[3]: 1.000000
(定量的に評価したわけではありませんが)
ステップを進めると精度が良くなっていくのがわかります
除算 (64bit ARMのみ)
サンプル
vdivq_f32を使用して32bit浮動小数ベクタva, vbの除算をやってみます
コンパイルする際は64bit用のコンパイラ(aarch64-linux-gnu-g++など)を使ってね
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> static void print_vector(float32x4_t value) { float lane[4]; vst1q_f32(lane, value); for (int i = 0; i < 4; i++) printf("lane[%d]: %f\n", i, lane[i]); } int main() { float a[4] = { 1, 2, 3, 4 }; float b[4] = { 1, 2, 3, 4 }; float32x4_t va = vld1q_f32(a); float32x4_t vb = vld1q_f32(b); float32x4_t vc = vdivq_f32(va, vb); printf("va:\n"); print_vector(va); printf("\nvb:\n"); print_vector(vb); printf("\nva / vb:\n"); print_vector(vc); return 0; }
実行結果
va: lane[0]: 1.000000 lane[1]: 2.000000 lane[2]: 3.000000 lane[3]: 4.000000 vb: lane[0]: 1.000000 lane[1]: 2.000000 lane[2]: 3.000000 lane[3]: 4.000000 va / vb: lane[0]: 1.000000 lane[1]: 1.000000 lane[2]: 1.000000 lane[3]: 1.000000
そのまま除算ができるとありがたいですね
また64bit ARM(ARMv8)では浮動小数のSIMD演算がIEEE754準拠になったため
結果もCPUと変わらないはずです
参考
NEONの32bitと64bitの違いが解説されてます
今回の記事を書くにあたりとても参考になりました
community.arm.com
次回
次回は初期化編です
ARM NEONの使い方 初期化編
Stixel Computationを実装してみた
6D-Visionについて調べてみたで紹介したStixelですが
ちまちまと実装を重ね、ようやくひと段落したので公開することにしました
使い方
README.mdに記載しましたので
興味があれば使ってやって下さい
アルゴリズム解説
執筆中…!
参考文献
- [1] D. Pfeiffer, U. Franke: “Efficient Representation of Traffic Scenes by means of Dynamic Stixels”, IEEE Intelligent Vehicles Symposium IV 2010, San Diego, CA, Juni 2010
- [2] H. Badino, U. Franke, and D. Pfeiffer, “The stixel world - a compact medium level representation of the 3d-world,” in DAGM Symposium, (Jena, Germany), September 2009.
ARM NEONの使い方 乗算編
今回は乗算編です
特に変わった内容はありません
乗算
サンプル
符号付き16bit整数ベクタの乗算をしてみます
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, 2, 3, 4 }; int16_t b[4] = { 5, 6, 7, 8 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int16x4_t vc = vmul_s16(va, vb); int16_t c[4]; vst1_s16(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); return 0; }
積和演算
みんな大好き(?)積和演算
内積とか計算するときに重宝しますね
サンプル
符号付き16bit整数のベクタの積和演算です
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, 1, 1, 1 }; int16_t b[4] = { 2, 2, 2, 2 }; int16_t c[4] = { 3, 3, 3, 3 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int16x4_t vc = vld1_s16(c); int16x4_t vd = vmla_s16(va, vb, vc); int16_t d[4]; vst1_s16(d, vd); for (int i = 0; i < 4; i++) printf("d[%d]: %d\n", i, d[i]); return 0; }
実行結果
d[0]: 7 d[1]: 7 d[2]: 7 d[3]: 7
doubling multiplyってなんぞや
乗算に関しては先ほどのmulとmlaを使うことがほとんどだと思いますが
命令一覧を見ると doubling multiply というのがあったので使ってみました
サンプル
vqdmull(Vector saturating doubling long multiply)を使って乗算をしてみると…
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, 2, 3, 4 }; int16_t b[4] = { 5, 6, 7, 8 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int32x4_t vc = vqdmull_s16(va, vb); int32_t c[4]; vst1q_s32(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); return 0; }
実行結果
c[0]: 10 c[1]: 24 c[2]: 42 c[3]: 64
結果が2倍になった
どうやら乗算してさらに2倍する演算のようです
使い道はあるのかな…
次回
次回は除算編です
ARM NEONの使い方 除算編
ARM NEONの使い方 減算編
年内に終わるかな?
今回は減算編です
減算 (通常の減算、符号拡張付き減算、飽和付き減算)
加算編で紹介したものとほぼ変わらないので、まとめて紹介
サンプル
符号付き16bit整数のベクタvaとvbの引き算を、先ほど紹介した3つの方法でやってみます
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, -1, 1, -2 }; int16_t b[4] = { 1, -1, -32767, 32767 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int16x4_t vc = vsub_s16(va, vb); int32x4_t vcl = vsubl_s16(va, vb); int16x4_t vcq = vqsub_s16(va, vb); printf("vsub_s16\n"); int16_t c[4]; vst1_s16(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); printf("\nvsubl_s16\n"); int32_t cl[4]; vst1q_s32(cl, vcl); for (int i = 0; i < 4; i++) printf("cl[%d]: %d\n", i, cl[i]); printf("\nvqsub_s16\n"); int16_t cq[4]; vst1_s16(cq, vcq); for (int i = 0; i < 4; i++) printf("cq[%d]: %d\n", i, cq[i]); return 0; }
実行結果
vsub_s16 c[0]: 0 c[1]: 0 c[2]: -32768 c[3]: 32767 vsubl_s16 cl[0]: 0 cl[1]: 0 cl[2]: 32768 cl[3]: -32769 vqsub_s16 cq[0]: 0 cq[1]: 0 cq[2]: 32767 cq[3]: -32768
3、4番目のレーンの引き算の結果がそれぞれ
- vsub_s16()ではオーバーフロー
- vsubl_s16()では32bitに拡張
- vqsub_s16()では最大値/最小値で飽和
となっています
符号なしベクタの減算について
符号なし16bit整数のベクタvaとvbの減算を考えます
このときvsub_u16()を使ってしまうと、戻り値も符号なし16bitなので
va[i] >= vb[i]の場合は正しい結果が得られるのですが
va[i] < vb[i]の場合はオーバーフローが発生してしまいます
正しい結果を得るためには、ベクタを符号付き32bitに拡張する必要がありますが、
これを1回で実現してくれるNEON命令はなさそうです
そこで1つ思いついたのが、vsubl_u16()を使用して減算結果を符号なし32bitに拡張し
vreinterpretq_s32_u32()で符号付き32bitとして解釈する方法です
サンプル
符号なし16bit整数のベクタvaとvbの引き算を、vsub_u16()を使った方法と
vsubl_u16() & vreinterpretq_s32_u32()を使った方法でやってみます
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { uint16_t a[4] = { 1, 1, 1, 1 }; uint16_t b[4] = { 0, 1, 2, 65535 }; uint16x4_t va = vld1_u16(a); uint16x4_t vb = vld1_u16(b); uint16x4_t vc = vsub_u16(va, vb); uint32x4_t vc_u32 = vsubl_u16(va, vb); int32x4_t vc_s32 = vreinterpretq_s32_u32(vc_u32); printf("vsub_u16\n"); uint16_t c[4]; vst1_u16(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); printf("\nvsubl_u16 and vreinterpretq_s32_u32\n"); int c_s32[4]; vst1q_s32(c_s32, vc_s32); for (int i = 0; i < 4; i++) printf("c_s32[%d]: %d\n", i, c_s32[i]); return 0; }
vsub_u16 c[0]: 1 c[1]: 0 c[2]: 65535 c[3]: 2 vsubl_u16 and vreinterpretq_s32_u32 c_s32[0]: 1 c_s32[1]: 0 c_s32[2]: -1 c_s32[3]: -65534
vsubl_u16() & vreinterpretq_s32_u32()を使った方法で、一応正しい結果が得られました
やり方として良いのかわかりませんが…
次回
次回は乗算編です
ARM NEONの使い方 乗算編
Free Space Computationを実装してみた
以前の記事で紹介したFree Space Computationですが
実装がひと段落したので公開することにしました
使い方
README.mdに記載しましたので
興味があれば使ってやって下さい
その他メモ
Road Disparity
[1]では路面上の視差をB-Splineでフィッティングして求めていますが
カメラパラメータから路面上の視差を計算する方法もあります([2]で知りました)
今回は計算が簡単なカメラパラメータを使う方法を採用しました
DPによる境界の計算
ここは割と推測で実装してる部分がありまして、あまり自身はありません
あと計算時間の都合上、かなり処理を端折ってる部分があります…
ARM NEONの使い方 加算編
四則演算編の予定でしたが、量が多いので分割することにしました
今回は加算編です
加算
サンプル
符号付き16bit整数のベクタvaとvbをvadd_s16()で足してみます
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, -1, 1, -1 }; int16_t b[4] = { 1, -1, 32767, -32768 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int16x4_t vc = vadd_s16(va, vb); int16_t c[4]; vst1_s16(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); return 0; }
実行結果
c[0]: 2 c[1]: -2 c[2]: -32768 c[3]: 32767
3,4番目のレーンはオーバーフローしました
符号拡張+加算(long add)
サンプル
符号付き16bit整数のベクタvaとvbをvaddl_s16()で足してみます
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, -1, 1, -1 }; int16_t b[4] = { 1, -1, 32767, -32768 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int32x4_t vc = vaddl_s16(va, vb); int32_t c[4]; vst1q_s32(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); return 0; }
実行結果
c[0]: 2 c[1]: -2 c[2]: 32768 c[3]: -32769
各レーンが32bitに拡張され、オーバーフローしなくなりました
飽和加算(saturating add)
vqadd[q]_<type>(va, vb)
64bit(qが付く場合は128bit)のベクタvaとvbを足します
演算結果がオーバーフローする場合は最大値/最小値で飽和させます
戻り値のサイズは入力のサイズと同じです
サンプル
符号付き16bit整数のベクタvaとvbをvqadd_s16()で足してみます
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int16_t a[4] = { 1, -1, 1, -1 }; int16_t b[4] = { 1, -1, 32767, -32768 }; int16x4_t va = vld1_s16(a); int16x4_t vb = vld1_s16(b); int16x4_t vc = vqadd_s16(va, vb); int16_t c[4]; vst1_s16(c, vc); for (int i = 0; i < 4; i++) printf("c[%d]: %d\n", i, c[i]); return 0; }
実行結果
c[0]: 2 c[1]: -2 c[2]: 32767 c[3]: -32768
3,4番目のレーンは最大値/最小値で飽和しました
その他の加算
個人的にあまり使わなそうだと思ったものですが
簡単に触れておきます
wide add: vaddw_<type>(va, vb)
サイズが違うもの同士を足す場合に使うようです
例えばvaddw_s16(va, vb)はvaがint32x4_tでvbがint16x4_tです
add high half: vaddhn_<type>(va, vb)
各レーンの上位ビット同士を足すようです
例えば、各レーンが32bitなら上位16bit同士を足します
どこで使うんだろう…
#include <stdio.h> #include <stdint.h> #include <arm_neon.h> int main() { int a[4] = { 0, 1, 2, 3 }; int b[4] = { 0, 1, 2, 3 }; for (int i = 0; i < 4; i++) { a[i] = a[i] << 16; b[i] = b[i] << 16; } int32x4_t va = vld1q_s32(a); int32x4_t vb = vld1q_s32(b); int16x4_t vc = vaddhn_s32(va, vb); // { 0, 2, 4, 6 } return 0; }
rounding add high half: vraddhn_<type>(va, vb)
これ、よく分かりませんw
(知ってたら教えて下さい)
次回
次回は減算編の予定です
ARM NEONの使い方 減算編